Игры с положительным исходом

Игра с нулевой суммой — это взаимодействие, в котором выигрыш одной из сторон равен проигрышу другой, то есть сумма выигрышей и проигрышей равна нулю (точнее, она постоянна для любых комбинаций их ходов). Квинтэссенция такой игры — спортивные соревнования: победа — это главная цель и единственный возможный исход, «хорошие парни» тут не выигрывают. Игра с ненулевой суммой — это взаимодействие, в котором некоторые комбинации ходов обеспечивают чистый выигрыш (положительный исход) или проигрыш (отрицательный исход) обоим игрокам. Типичным ее примером служит торговля излишками, когда пастухи и фермеры меняют шерсть и молоко на зерно и фрукты, или торговля услугами, когда родители по очереди сидят с детьми друг друга.

В игре с нулевым исходом рациональный субъект, который ищет для себя максимально возможный выигрыш, непременно будет добиваться максимального проигрыша для второго субъекта. В игре с положительным исходом рациональный, движимый личными интересами субъект может помочь другому, сделав выбор, который будет выгоден ему самому. Проще говоря, играми с положительным исходом называются беспроигрышные для обеих сторон ситуации, зафиксированные в клише «проигравших нет» (win-win). Этот набор понятий (игры с нулевым, ненулевым, положительным, отрицательным, постоянным и переменным исходом) впервые был предложен Джоном фон Нейманом и Оскаром Моргенштерном при создании ими математической теории игр в 1944 году.

Когда люди взаимодействуют между собой, их выбор не определяет нулевой или ненулевой исход игры; игра — это часть мира, в котором они живут. Но, упуская из виду некоторые варианты, люди могут чувствовать, что они играют в игру с нулевым исходом, хотя на деле исход ненулевой. Кроме того, окружающий мир можно специально менять так, чтобы исход взаимодействия стал ненулевым. Если люди осознают теоретико-игровую структуру своего взаимодействия (имеет ли оно положительный, отрицательный или нулевой исход), они могут делать выбор, который принесет им безопасность, гармонию и процветание, и при этом сами они вовсе не станут от этого более добродетельными, благородными или безупречными.

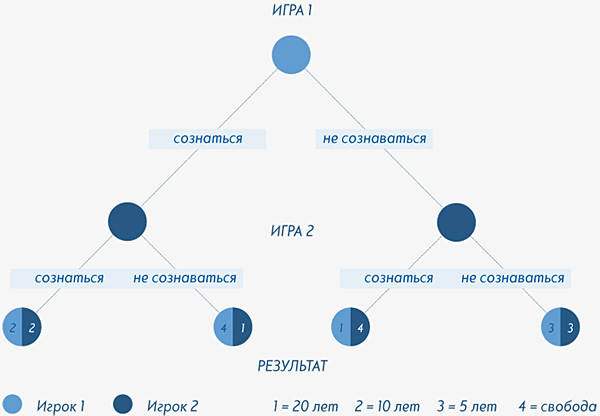
Каноническим примером игры с ненулевой суммой считается «дилемма заключенного»:
двум предполагаемым сообщникам предлагают дать показания против другого.
Если № 1 сознается, а № 2 — нет, № 1 получает свободу, а № 2 — 20 лет.
Если сознаются оба, то оба получают по 10 лет за преступление в сговоре,
но если оба молчат, то оба получают 5 лет. Если представить ее как последовательность
двух игр (см. схему), выгода сотрудничества между заключенными становится очевидна.

Примеры тут могут быть самые разные. Когда две стороны на переговорах идут на компромисс, чтобы добиться согласия. Когда супружеская пара, оформляющая развод, понимает, что можно уйти от схемы, при которой каждый стремится заткнуть за пояс другого, к схеме, при которой каждый стремится сберечь как можно больше собственных денег от адвокатов Дьюи, Читэма и Хау. Когда простой народ осознает, что экономические посредники (особенно этнические меньшинства, специализирующиеся в этой нише, такие, как евреи, армяне или китайцы из диаспоры) не общественные паразиты, чье процветание обеспечивается за счет принимающего общества, а творцы взаимодействий с положительным исходом, которые одновременно обогащают всех. Когда страны признают, что международная торговля не несет выгоду их торговому партнеру им самим в ущерб, а выгодна обеим сторонам, и отказываются от протекционистской политики «разорения соседа» в пользу открытой экономики, которая (как отмечали экономисты-классики) всех делает богаче и (как недавно показали политологи) предотвращает войну и геноцид.

Допустим, некоторые процессы взаимодействия между людьми на самом деле имеют нулевой исход: яркий пример из биологии — борьба за самку. И даже в играх с положительным исходом одна из сторон может преследовать личную выгоду в ущерб совместному благополучию. Однако осознание в полном объеме рисков и издержек теоретико-игровой структуры взаимодействия (а особенно — ситуаций, когда соблазн получения выгоды на одном этапе может привести к невыгодному положению на следующем, когда роли изменятся) может препятствовать различным формам недальновидного использования второй стороны в своих интересах.

И все-таки привела ли нарастающая с 1950-х годов осведомленность общества о взаимодействиях с нулевым и ненулевым исходами к миру и процветанию на планете? В большей степени, чем может показаться. Международная торговля и членство в международных организациях резко выросли за десятилетия, когда теоретико-игровое мышление начало проникать в массовый дискурс. И, возможно, не случайно развитый мир переживает и впечатляющий экономический рост, и беспрецедентный в истории спад ряда проявлений институционализированного насилия, такого, как война между сверхдержавами, война между богатыми странами, геноцид, смертоносные этнические мятежи. С 1990-х такие подарки начали перепадать и развивающемуся миру.

Биологи Джон Мейнард Смит и Эорс Сатмари утверждают, что эволюционная динамика, создающая игры с положительным исходом, обусловила основные переходы в истории жизни: возникновение генов, хромосом, бактерий, клеток с ядром, организмов, полового размножения, животных сообществ. При каждом переходе биологические агенты входили в большие системы, в которых они специализировались, приносили и получали пользу, а также совершенствовали защитные механизмы с целью предотвратить эксплуатацию одной составляющей остальных в ущерб целому. Журналист Роберт Райт наметил схожую линию в книге «Не-ноль: логика судьбы человечества» и расширил ее, применив к далекой истории человеческих обществ. Явное признание среди образованных людей сокращенной абстрактной конструкции «игра с положительным исходом» и близких понятий может быть распространением процесса, который действует в мире природы уже миллиарды лет, в сферу присущего человеку выбора.

Автор:
Стивен Пинкер,
психолог, нейролингвист, профессор Гарвардского университета
esquire.ru